Звёздной  Рассе Х’Арийцев, создавших такую удивительную Х’Арийскую арифметику

эта статья посвящается

Как известно, Нобель всем, кроме математиков, установил премии – просто потому, что математик увёл у него любимую. Нобель был дважды прав, поскольку почти все математики мира путают операцию вычитания с отрицательными числами. Вот платить бы им жалование отрицательными  или мнимыми буханками хлеба сразу бы поумнели. Отрицательных чисел в природе нет, так как нечего уже вычитать. Есть величины противоположные, но для этого нужно задать два движения. Например, электрон - это тороид, где вращение эфира идёт как по кругу, так и внутри тора. Вот теперь можно ввести право и лево, хотя слова не имеют значение. Позитрон, такое же образование, но одно вращение идёт в противоположную сторону. Другой пример. Фотон – здесь вращение и поступательное движение. Фотоны как известно имеют две поляризации, выходит, что это две античастицы, а современная наука, утверждает, что фотон не имеет антицастицы. Короче, современная математика – безобразная, то есть без образа. А есть ли другая? Конечно – это Х’Аррийская арифметика наших предков. Демокрит утверждал, что весь мир состоит из неделимых частиц и был абсолютно прав, только вот по злому умыслу это интерпретировали, как атом - а он имел ввиду эфир. Тогда получается интерестная вещь – мы не можем так просто использовать дифференциальное и интегральное исчисление, поскольку оно предполагает деление до безконечности.

Давайте теперь возьмём две точки и соединим их прямой. Назовём это единицей. Создадим теперь реплику её. Получили двойку, но ведь из чего то- если к примеру единичку сделали из верёвки или дерева, то чтоб создать реплику потребуется материал. Можем ли мы продолжать процесс репликации до бесконечности – нет, конечно- исходного материала не будет, да и время требуется. Отсюда истекает простой вывод – бесконечностей в нашем мире нет иначе этого мира бы не было.

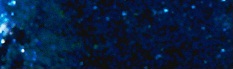
Давайте теперь из нашей единицы сделаем перпендикулярную проекцию- получим квадрат (Рис 1). Если из двойки сделать проекцию, то получим квадрат, состоящий из четырёх одинаковых квадратиков. Для тройки получаем квадрат, состоящий из 9 квадратиков, но тех же самых. Теперь перейдём к сложению целых чисел, которые мы выразили вот таким геометрическим образом. Для пространства первого порядка всё вроде бы понятно. Весь натуральный ряд состоит из одних и тех же отрезков и при суммировании мы получаем элемент этого же пространства. Это и есть условие сложения в целых числах.

Рис. 1 Отрезок – первая проекция точки. Квадрат – вторая проекции точки. Куб – третья проекция.

Другое дело для квадратичного пространства – складывать мы в принципе можем, но появляются ограничения на колличество слагаемых – два квадрата в сумме дают квадрат только в определённых случаях (3² + 4²= 5²) , но любую фигуру этого пространства всегда можно сложить из одних и тех же квадратов, как я уже упомянул 2² легко складывается из 4-х единичных квадратиков. Когда мы говорим, что 2²=4 это собственно говоря не верно, хотя бы потому, что если взять за единицу один метр, четыре м² не может равнятся четырём метрам линейным. Вот когда мы складываем 4 метра с 2–мя метрами – всё корректно, также как и когда складываются м² с м². А что происходит, когда мы складываем  м² с м. Так просто это не сделаешь- по сути мы делаем для м² обратную операцию и возвращаемся в линейное пространство. Теперь мы можем складывать в линейном пространстве, поскольку исходная единичка одна и таже, но получаем мы уже элемент этого линейного пространства. Не понимание этого, приводит к глупейшим математическим казусам, типа 1= 1²=1³ ...Можете себе представить, чтоб 1 м был равен 1м² ещё и 1м³? Это противоречит самим конам математики, что сравнивать можно величины, состоящие из одних и тех же элементов.

Сделаем ещё одну перпендикулярную проекцию. Для 1-го квадрата получим куб со стороной 1 из линейного пространства. Для двойки получим куб, состоящий из восьми кубиков, для 3 – из 27 кубиков и т.д. Мы тоже можем складывать в этом пространстве 3-ей степени, поскольку все элементы этого пространства одни и теже, но ограничений появляется больше. Будем считать, чтоб не загромождать статью, что Великая Теорема Ферма доказана для третьей степени- это означает, что нельзя сложить два куба и получить новый куб, ну а три или четыре куба – уже можно. То есть на операцию сложения накладываются дополнительные ограничения, которые можно вывести.

Перейдём к пространству четрёртой степени. Для этого нужно для чила Х сделать  Х реплик Х³ и мы уже получаем опять линейное пространство, но единичкой этого пространства будет Х³. Например, для 2-ки будет два куба, состоящих из 8 кубиков каждый. Для 3-ки -3 кубика, каждый из которых имеет 27 кубиков и т.д. Можем ли мы складывать в этом линейном пространстве – ни в коем разе- операция сложения для целых чисел потеряла смысл, поскольку элементы этого пространства разные.  По другому говоря, возведение в четвёртую степень какого либа числа Х, порождает собственное линейное пространство с ограниченным колличеством элементов, где единицей служит куб этого числа Х³, а число элементов этого пространства равно Х (Рис. 2). Внутри каждого такого  пространства операция сложения работает, а вот складавать два таких пространства не имеет смысла. Ну как вы сложите три стакана, например с тремя чашками под чай? И стаканы и чашки сделаны из одного материала- стекла, но складывать мы их не можем. Чтоб сложить их, мы должны свернуть эти пространства к исходному – линейному. Здесь встаёт вопрос  что понимать под сложением в таком пространстве – можно ли  сложить поэлементно два таких пространства , чтоб получить элемент этого же пространства – ни коим образом, поскольку при сложении двух кубов, куба не получается да и число элементов разное. Ну а если сладывать больше чем два элемента – вполне реально, поскольку из большего колличества кубиков можно создать новый кубик, правда это уже не операция сложения в привычном понимании.

Рис. 2 Операция возведения в степень на примере тройки.

Возведение в 5-у степень порождает квадратчное пространство, аналогичное степени 2, но элементами этого пространства являются кубики 3-х мерного. Собственно говоря, пространства 5 степени ,это квадратичные матрицы, где размер матрицы определяется числом из пространства первого порядка, а элементами этого пространства являются кубики третьего пространства. Можно ли сложить две матрицы состоящие из разных кубиков да ещё и имеющие разные размеры, чтоб получить новую матрицу такого же пространства? Нет, по тем же самым причинам, что и для 4-й степени – два куба сложить не возможно.

Что происходит дальше – повторение трёх изначальных пространств или в более общем виде для числа Х в степени кратной трём имеем   кубическое пространство, элементами которого являются кубики из линейного пространства на степени в два раза меньше, а пространство на единицу меньше – это квадратичные матрицы из тех же элементов. Вот и вся теорема Ферма – из невозможности сложить два куба в трёхмерном пространстве чтоб получить куб, следует что их невозможно сложить для больших степеней. Может быть именно это доказательство и имел ввиду Ферма, когда оставил запись на полях книги.

Такое геометрическое представление операции возведения в степень приводит к совершенно неожиданному пониманию, что такое движение и покой материального тела, а также что такое время. Состояние покоя – это репликация объекта с очень большой скоростью, и эта скорость и есть время. При движении скорость репликации увеличивается и объект становится твёрже. Вас не удивляет, что свинцовая пуля пробивает стальные доспехи? Свинец же мягче стали. А когда каратист разбивает кирпичи рукой уже как то загадочно выглядит, не правда ли? При ускорении тела число реплик увеличивается и колличество движения или импульс можно интерпретировать, как величину кратную колличеству реплик. При торможении колличество реплик возвращается к исходному и это и есть инерция.

Такой цифровой подход может показаться необычным, но вас же не удивляет когда вы слушаете сиди диски или смотрите дивиди.

Чтоб такой мир существовал, необходимо иметь как минимум ещё одну материю наложенную на первую, которая бы управляла скоростью репликации. Здесь встаёт вопрос – а у животных и человека можно ли изменять скорость репликации? Ну во первых- она уже разная. Сравните кошку и черепаху к примеру – у них разное собственное время. Человек же может увеличивать скорость репликации сознательно- в этом случае он  за несколько минут может прожить месяцы. Мир для него станет как в замедленной киносъёмке, а для окружающих он исчезнет из виду, такое можно сравнить с пропеллером- когда он вращается с большой скоростью лопасти перестают быть видны, зато вы можете видеть сквозь них. Естественно человек в таком состоянии теряет в весе за минуты как за месяцы голодания. Тело его станет необычно твёрдым  в таком состоянии. Ну а теперь сравните это с рассказом человека, который делал это много раз - это характерник.

Я тоже разбивал кирпичи и доски с целью понять, как это происходит - ну совсем не так, как описывают. Резкость удара, конечно нужна, но не это главное. В мозге человека есть железа, которая позволяет изменять течение времени, но чтоб активировать её нужно войти в состояние между жизнью и смертью - на лезвии бритвы, как в известном романе Ефремова. Я понял это, когда занимался бегом на длинные дистанции. Тренировка была простой – прыгаешь в канаву, где сидят зайцы и бежишь, что есть сил за ним, пытаясь схватить за уши. На определённом этапе, включается что то типа второго дыхания – ты уже не бежишь, а летишь, преодалевая несколько десятков метров в прыжке. Как только я понял это, я за одно лето стал чемпионом почти во всех видах лёгкой атлетики, естественно не в мировых состязаниях – это была Прага, центральная группа войск. Другой способ - это задержка дыхания под водой. Я до сих пор могу легко пронырнуть метров 50.  Гарри Улер в автобиографической книге описывает нечто подобное, когда он бежал, опаздывая куда то и вдруг полетел и разбил телом стекло в месте назначения.

Можно ли техническими средствами изменить ход времени? Это уже делалось не раз.

Первый известный эксперимент– это Филадельфийский эксперимент и первый, кто додумался до зтого – Никола Тесла, поскольку вся аппаратура была сделана им. Эйнштейн же видимо вообще не понимал, что делается, поскольку Тесла настаивал на дополнительной защите людей, а Эйнштейну было наплевать на это-сроки поджимали. Как вообще объект можно сделать невидимым- первое – остановить репликацию, второе- сильно ускорить и двигать его. Тесла похоже избрал второй способ.

Можно ли попасть в будущее или прошлое? В прошлое ну никоим образом, можно лишь увидить запись. В будущее – ну без проблем, замедлите скорость собственной репликации и всё. Но живём мы в настоящем, которое можно назвать мигом (сигом) между прошлым и будущим.

Алексей Воеводский

Торонто.

Источник